近日,MIT-哈佛超冷原子研究团队创新性地开发了名为“全局相位光谱(global-phase spectroscopy)”技术,利用量子纠缠放大信号,实现了标准量子极限的突破,直接测量得到了2.4(7)dB的计量增益和4.0(8)dB的激光噪声灵敏度改善。相关工作以“Quantum-amplified global-phase spectroscopy on an optical clock transition”为题发表在国际学术期刊《自然》(Nature)上[1]。

© Nature
光学晶格钟是当今最精密的计时工具,其稳定性和精度已接近由量子噪声决定的标准量子极限(SQL)。虽然理论上利用量子纠缠可以突破这一限制,但在实际应用中,面临着可扩展性、测量分辨率以及如何保持纠缠态稳定性等诸多困难。
标准量子极限来自于量子力学的概率性基本原理,突破这一极限需要将光晶格中大量原子纠缠在一起,同时保证纠缠态寿命和探测精度,但在实验上难以实现。最近,有研究已在GHZ纠缠态上已实现低于SQL的频率稳定度[2,3,4],但难以规模化。另一方面,自旋压缩态有望被用于突破SQL,相对GHZ态,它的相干时间更长,但难点在于态探测需要达到低于量子投影噪声级别的分辨率。
对此,该研究团队利用量子纠缠,构建了一种Rabi型的“全局相位光谱(GPS)”取代传统的Ramsey光谱技术。该方法基于驱动循环演化,使驱动的光学量子比特获得Aharonov-Anandan全局相位,在基态间实现了对失谐敏感的完整量子相位门。
这种创新GPS技术首次将纠缠增强拓展至Rabi型光谱领域。虽然对本振激光噪声的直流灵敏度与传统Rabi光谱相当,但GPS对高频的相位(频率)噪声的敏感度呈现∝f -4 (∝f -6 )的优异特性,显著优于传统Rabi光谱的∝f -2 (∝f -4 )和Ramsey光谱的∝f 0 (∝f -2 )。更关键的是,传统Rabi光谱通过测量布居数不平衡且需偏频操作,而GPS直接测量相位并在共振点时获得最大灵敏度,这为反馈控制提供了理想条件。这一特性也使GPS能与共振旋转回波技术(rotary echo)结合,有效重聚焦光-原子耦合的不均匀性,为复合脉冲序列的实施提供了新的技术路径。
通过以上方法,研究团队利用在二维光晶格中N=2.2(4)×102个171Yb原子,在单一系综中对两个钟跃迁进行差分测量。通过时间反演协议对压缩探测态记录的差分相位进行放大,最终实现了低于标准量子极限2.4(7) dB的计量增益(扣除残余激光噪声后可达4.0(8) dB)。这是在具有全局纠缠相互作用的中性原子系统中首次实现此类突破。
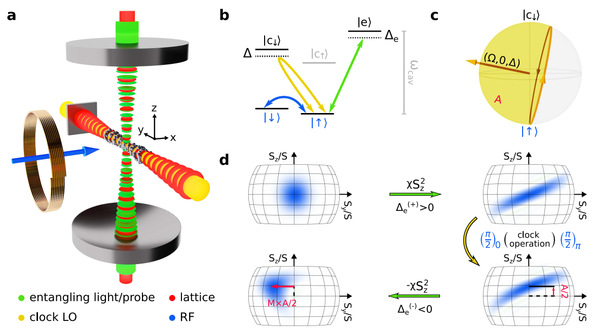
图1. 纠缠时间反演全局相位光谱的实验装置和原理
(a)激光冷却的原子被囚禁在高精细度光学腔内的二维光晶格中
(b)171Yb原子参与GPS的能级图
(c)在GPS过程中,钟激光驱动原子态在Bloch球上沿着黄色曲线做封闭运动,积累的Aharonov-Anandan相位是封闭曲线面积的一半
(d)基于时间反演的量子放大原理示意图
《自然》杂质的审稿人称赞该研究引入了“一系列极具巧思的技术方案(very clever techniques)”,以其“有望移植至实际尖端光学晶格钟系统(have the potential to be transferred to actual state-of-the-art optical lattice clocks)”是“量子计量研究前沿领域的重要贡献(a significant contribution at the forefront of quantum metrology research)”。文章中也写道“预计该技术将广泛应用于接近量子精度极限的新一代原子钟及其他量子传感器领域(We expect it to be broadly applicable to next-generation atomic clocks and other quantum sensors approaching the fundamental quantum precision limits)”。
可以预见,该创新性的方法将推动精密测量的发展越过标准量子极限的大门,让科学家从“测量已知”走向“探测未知”,用一把更精密的“尺”去探索洛伦兹对称不变形破缺、暗物质、宇宙物理学常数的变化等新物理领域。
[1] Zaporski, L., Liu, Q., Velez, G. et al. “Quantum-amplified global-phase spectroscopy on an optical clock transition”, Nature 646, 309–314 (2025).
[2] Song, C. et al. “Generation of multicomponent atomic Schrödinger cat states of up to 20 qubits”, Science 365, 574–577 (2019).
[3] Omran, A. et al. “Generation and manipulation of Schrödinger cat states in Rydberg atom arrays”, Science 365, 570–574 (2019).
[4] Finkelstein, R. et al. “Universal quantum operations and ancilla-based read-out for tweezer clocks”, Nature 634, 321–327 (2024).
