谷歌 DQI：纠错码还能兼职加速量子计算？

来源：Nature发布时间：2025-10-29

　　实现优化问题的超多项式加速一直是量子算法的核心目标。组合优化领域在过去三十年里一直将量子算法作研究的热点[1]，科学家们致力于寻找能在组合优化问题上实现超多项式加速的量子算法。近日，Google Quantum AI团队开发了一种“解码量子干涉测量（Decoded Quantum Interferometry，简称 DQI）”的全新量子算法。在max-XORSAT问题中 DQI 找到近似最优解的速度远快于通用经典启发式算法。当在有限域上解决近似最优多项式拟合问题时，DQI 相对已知经典算法实现了超多项式加速。相关研究论文于2025年10月22日“Optimization by decoded quantum interferometry”为题发表在国际学术期刊《Nature》上[Nature 646, 831 (2025)]。

　　要理解这一突破的意义，我们不妨先了解什么是“无法计算”的问题。假设现在某宝“双十一”开始了，一如既往地推出了规则复杂的优惠活动：有四个商品，你可以选择买其中的1/2/3/4个，根据不同的购买组合，有不同的优惠。

优惠活动规则举例

　　为了拿到最大优惠，你可能会穷举16种商品组合，并计算他们各自的优惠，然后选出最优的方案。计算16种组合只需要花你几分钟时间，是值得一算的。但如果现在有1000个商品和1000条规则，就产生了21000种方案——10的301次方)之多，哪怕用目前最快的超级计算机，穷举一遍也需要远超宇宙年龄的时间。类似这样的问题被叫做max-XORSAT问题，是让科学家头疼的“不可计算”问题之一。给max-XORSAT问题寻找最优解的耗时随着问题的变量规模呈指数爆炸型增长，因此穷举的方法必定不是长久之计。

　　为应对这一难题，在经典计算机上，科学家可以设计一些聪明的算法来尽可能高效地找到较优解。而崭新的量子计算领域也提供了QAA（量子绝热算法）、QAOA（量子近似优化算法）等计算工具，它们都极大的优化了解决max-XORSAT的速度与准确率。下图为经典和量子算法搜索最优方案的典型特征示意图，越深的谷代表越好的方案。

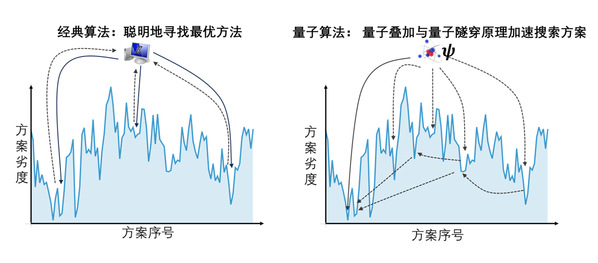
经典和量子算法搜索最优方案的典型特征示意图

　　但科学家们对经典算法以及传统的量子算法的效率依然感到不满意，但又暂时找不到更好的方法来解决max-XORSAT问题。难道我们只能止步于此了吗？2024年，谷歌量子AI团队给出了否定答案：“不，我们现在有了DQI算法！”

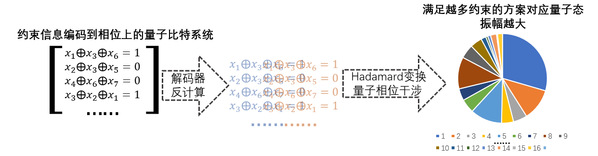
DQI算法特征示意图

　　DQI技术把问题的约束直接编码到量子态上，再用纠错码的解码技术实现反计算（uncomputation）而消除会影响量子干涉过程的中间态。最后，带有约束信息的量子系统产生干涉，满足约束条件最多的方案在干涉过程中会获得最大的振幅，自然地“浮出水面”。相较已有的经典乃至量子算法而言，DQI算法与经典解码器的合作绝对是令人耳目一新的想法。解码技术在这个过程中起到了非常关键的作用。因为反计算的过程中涉及到欠定线性方程组，其恰好对应着经典纠错码中的“伴随式（syndrome）解码问题”。而经典解码的技术已经相对成熟，可以仔细选择与问题的数学结构最适配的解码器，进而高概率地完成反计算[2]。

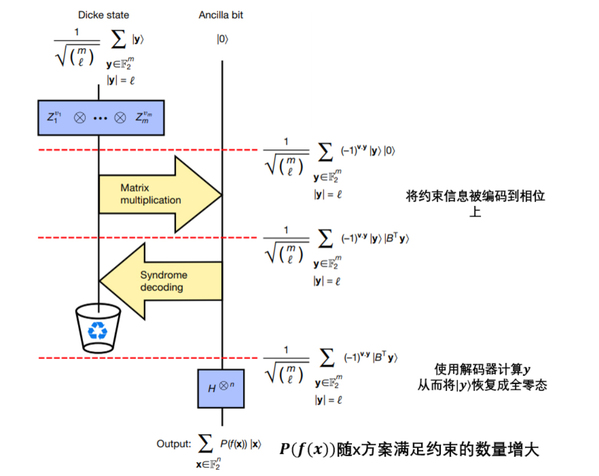
DQI算法实现流程

　　为验证DQI的性能，研究团队在含有31,216个变量与50,000个约束的max-XORSAT问题上，DQI技术配合信念传播（BP）解码方法，可以在8秒时间找到满足83.1%约束的方案。虽然满足率没有超过专门为max-XORSAT问题定制的Tailored heuristic算法，但耗时远短于Tailored heuristic的7分钟。

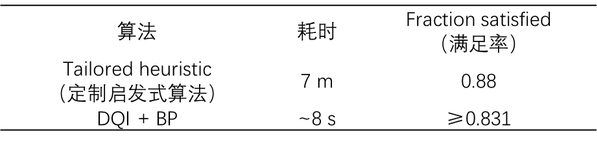
DQI+BP与定制启发式算法对比

　　若与退火算法（一种常用且较为普适的算法）对比，限定8秒的求解时间下，退火算法只能给出76.4%的满足率，显著低于DQI+BP算法。如果退火算法要达到83.2%的满足率，需要73小时的漫长时间来寻找，并且需要同时占用5个CPU核心（其他算法只用1个核心）。

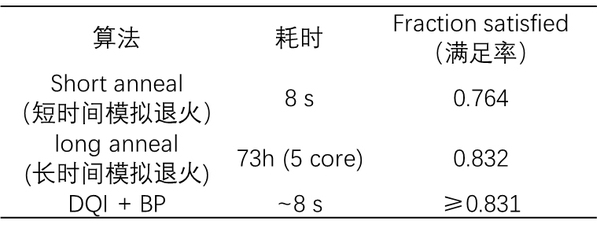
DIQ+BP与退火算法对比

　　从这些结果来看，DQI结合BP解码作为刚提出的算法，是非常具有潜力的。尤其是它创新地将编码解码技术融入到计算过程里，这将会给量子算法领域带来许多的新思路。不仅如此，研究发现，DQI算法在满足一些限定条件的最优多项式交集（Optimal Polynomial Intersection，OPI）问题中，对所有已知经典算法都实现了超多项式级加速。

　　需要特别注意的是理解以上具体例子对比的公平性。DQI+BP的8秒是指在经典计算机上模拟DQI量子算法中间的经典解码器的性能，仅用于估计满足率。而这并没有得到问题具体的解，而作为对比的经典启发式优化算法是实实在在的计算得到问题的解。DQI量子算法要得到问题的解，需要在容错量子计算机上运行完整的DQI算法，特别是中间的解码算法的实现需要用可逆量子线路来模拟经典运行，因此需要考虑CPU和量子处理器（QPU）的时钟频率差异、可逆编译的开销和容错开销（这个例子需要几万个逻辑比特，对应几千万个物理比特），总时间预计超过73小时。同时，DQI的优势目前仅限于“有代数结构或稀疏约束的问题”。对于没有固定结构的问题（如随机图的最大独立集、无规律的旅行商问题），目前DQI算法还没有办法加速计算。

　　参考文献

　　[1] Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–475 (2001).

　　[2] Jordan, S.P., Shutty, N., Wootters, M. et al. Optimization by decoded quantum interferometry. Nature 646, 831–836 (2025). 


相关文章